════════════════════

 

ANSWER: (No Peeking!)

• V_b - V_a = ∆V
• ∆U=q∆V
• W = q∆V = -U_E
• V = k_e∑q_i/r_i (between some point in space and each charged particle present in that region of space)
• V = ∫k_edq/r

YIIIKKEEEESSSSS... but Mr W, my brain is gonna implode!

Mine too.... flash cards, quizzing your comrades etc etc... gotta do it!

Let's take a gander at example 25.1 (that's pretty straight forward)

Now let's take a looksee at example 25.2

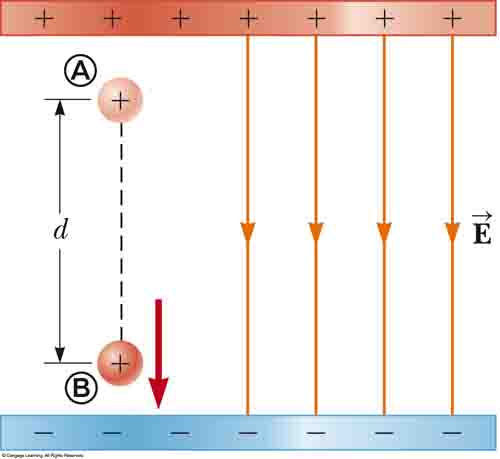
On the few days that we actually had class (so to speak!) there was some question about what the heck a *Uniform* electric field might be.

Our impression was that "uniform" means that the electric field has the same value at each point on the efield line:

It turns out that if we have two charged plates with equal but opposite charged surfaces, that the efield lines between them are, to a fairly high degree, uniform (if you are curious, check out example 23.9 and especially the bottom of example 24.5 to see that the Efield between two equally charged plates is σ/ε_o. Notice the Efield is position independent.

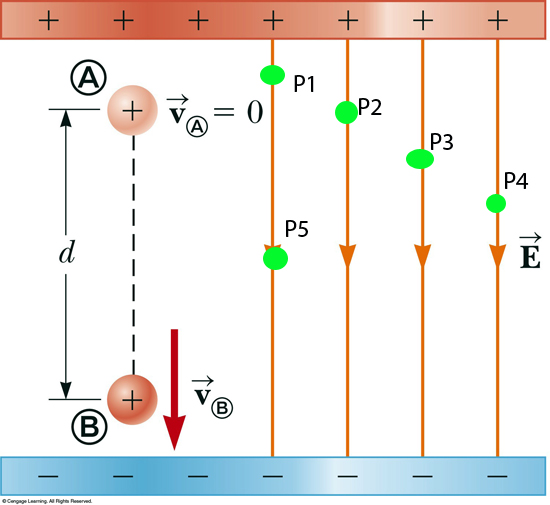
That means a trusty dusty test particle dropped in to our Uniform Efield at various points shown will experience the same electric field.

See example 25.1... that is a bit more predictable.

If your brain still hurts then just keep in mind that there IS such a thing as a Uniform electric field between two equally charged plates.

════════════════════

Ok... enough of that... let's see if we can tie in a bunch of what we've talked about so far.

Problem 25.19 is helpful here... Do That!